Introduction to Electric Force
In the previous tutorial, we have seen about Electric Charges and its significance in electricity. Let us continue exploring this concept further. But before that, let us go back to seventeenth century. Because, it was the time when “they” discovered that matter exerts force on each other. This force is a long-distance interaction between astronomical masses and is inversely proportional to the square of the distance between them. You might have guessed this force by now. It is Gravitational Force. But what about the interaction between two small objects at a small distance? It definitely is not gravitation as it is very weak in that dimension. Observations made by scholars shows that this “force” is also similar to gravitation only in the sense that it is also inversely proportional to the square of the distance between them. The similarity ends here and the differences start to show up. In gravitation, the force is always attractive in nature i.e. matter attracts another matter. But in short-range force, depending on a special property of the objects, the small things may attract or repel each other. The “thing” which cause these short-distance interactions is known as Electric Charge and the force between them is called Electric Force.
Statement of Coulomb’s Law
Coulomb’s Law is a quantitative statement about the force between two point charges. According to Coulomb’s, the force between two point charges q1 and q2:
Acts along the line joining the two point charges. Is proportional to the product of the two charges (q1.q2) Is proportional to the inverse of the square of the distance between the two charges.
Understanding Coulomb’s Law
In the late eighteenth century, a French Physicist named Charles de Coulomb experimented on the force between two charges. These two charges we considered to be point charges (theoretically, a point charge is an object whose electric charge is spread on a surface with a dimension infinitesimally small i.e. it has a location but no dimension). Consider two tiny charged objects that are modelled as point charges. If these two charged objects are brought near each other, then they exert a force on each other known as Electric Force. Let the two charged objects has an electric charge of q1 and q2 respectively. If the two point charges are separated by a distance r, then the magnitude of the electric force between the two point charges is F ∝ (q1 x q2) / r2
Constant of Proportionality (k)
According to Coulomb’s Law, the force between the two point charges mentioned above is dependent on the medium in which two charges are located and the effect of medium on the force is brought into the mathematical equation of electric force by a constant of proportionality denoted by k. So, the equation of coulomb’s Law becomes: F = k x (q1 x q2) / r2 As per SI units, the charges q1 and q2 have units of Coulomb (C), the distance r has units meters (m) and the Force F has units Newton (N). To compensate these and also satisfy the Coulomb’s Law, the proportionality constant k is defined as follows: k = 1 / (4πε) where ε is the permittivity of the medium in which the two point charges are located. The SI units of ε are Farad per meter (F/m). In general, the permittivity of a medium is expressed as follows: ε = ε0 εr where, ε0 is the permittivity of the free space εr is the relative permittivity of the medium with respect to the free space (it is also known as dielectric constant of the medium). If the medium is free space or vacuum, then ε = ε0 εr = 1. Then the electric force can be expressed as F = (1/4πε0) x (q1.q2) / r2 Further, the permittivity of free space ε0 has a value of: ε0 = (1/36π) x 10-9 F/m = 8.854 x 10-12 F/m.
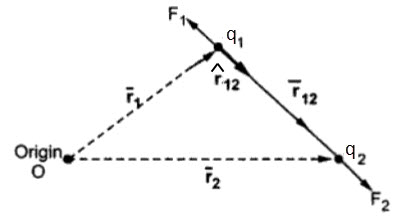
Vector Form of Coulomb’s Law
As mentioned in the statement, the force exerted between two point charges is directional and it acts along the line joining the two charges. This directional behavior leads to a vector representation of the force. Now, consider two point charges q1 and q2 located at two points with positional vectors r1 and r2. The force acts along the direction r12. The vector representation of the force is as follows:
where, r12 is the unit vector along the direction r12.
Comparison with Newton’s Equation
If you remember the Newton’s equation for gravitational forces between two objects of masses m1 and m2 that are separated by a distance r:
The coulomb’s constant k is analogous to Gravitational constant G. Both the equations describe the inverse square law with respect to the distance between the objects. The difference is the properties of the objects i.e. electric charge in Coulomb’s Law and mass in Newton’s Equation. The other difference (and the main one) is that Gravitational Force is always attractive while Electric Force is either attractive or repulsive.
Properties of Coulomb’s Law
Some of the important properties of Coulomb’s Law are given below:
For like charges, the electric force between them is repulsive and for unlike charges, the force is attractive. From mathematical point of view, this can be determined by the sign of the product q1.q2 in the numerator of the force equation. When the product q1.q2 is positive (in case of like charges), the force F is positive and pushes the charges away from each other. The product q1.q2 is negative for unlike charges and the force F is negative. This means the objects are attracted to each other. We have already seen the similarities between Electric Force and Gravitational Force. Bot the forces exhibit a 1/r2 property. This means that similar to planet orbiting the Sun, a negative charge can orbit around a positive charge. Although the main difference is that gravitation is always attractive while electric force can be either attractive or repulsive. The magnitude of the force F is exerted on both the objects. If a force of magnitude F is exerted on a charged object q1 then, a force of same magnitude F is exerted on q2 but in opposite direction.
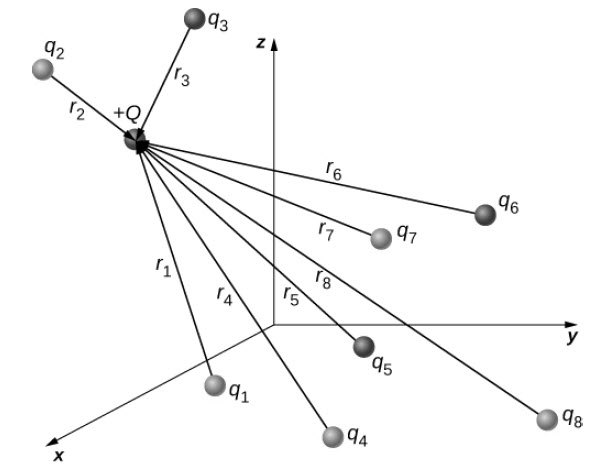
Force due to n number of Charges (Superposition of Electric Forces)
The discussion so far assumes that there are only two point charges and we calculated the force exerted on them. What if there are n number of charges? How can we use Coulomb’s Law to deal with such complex distribution of charges? It is very simple. We just repeat the analysis for two charges at a time.
Principle of Superposition is applied to calculate the net force on a charge. According to this, the net charge on a charge is simply the vector sum of the individual force exerted on it by other individual charges.
Here, Q is the test point charge which is experiencing the force F and qi are the ‘n’ source charges located at ri. Comment * Name * Email * Website
Δ



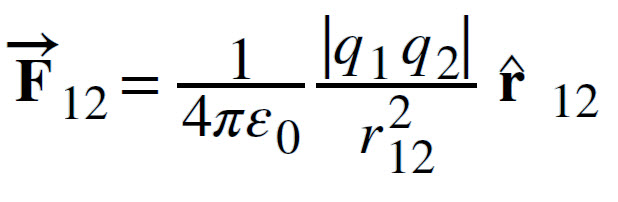
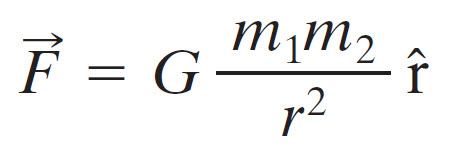
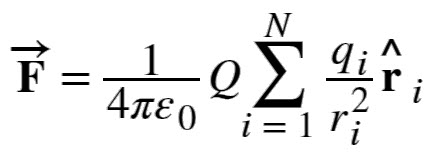


![]()